大学受験リード数学科の岸谷です。
今回は高校数学の取り組み方について何回かに分けてお話していくシリーズの1回目です。
今回のテーマは『覚えない数学』です。貴重な記憶容量、数学の公式で無駄にしていませんか?
定義は重要な約束事
早速ですが、次の文章を読んでみてください。
「x軸の正の部分を反時計回りに動径θ(シータ)回転した半直線と単位円との交点のx座標をcosθ、y座標をsinθ、y座標/x座標の値をtanθとする。」 これを読んだ皆様は下記のような図がすぐに思い浮かんだでしょうか。
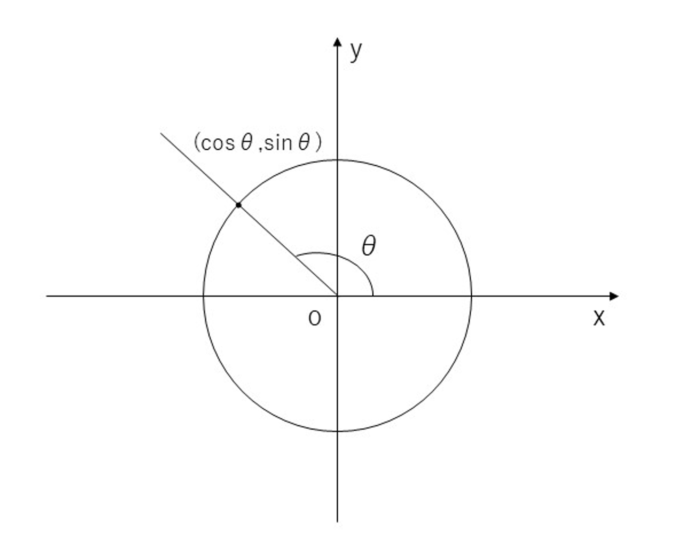
先ほどの文章は三角関数の定義ですが、単に覚えるだけはなく、この図とセットでイメージできるようにしておく必要があります。(余談ではありますが1999年の東大入試でsinθ、cosθの定義を述べよ、といった出題がなされ、話題になりました。続く問(2)の三角関数の加法定理の証明と合わせて、出来は非常に悪かったようです。)
なぜこの話題を取り上げたのか、お察しの通り、私の指導中においても、三角関数の定義について、ちゃんと述べられる生徒が少ないからです。
教科書の三角関数の章、2ページ目くらいに書いてある内容なのですが、それすらも『知らない』まま三角関数を学習していることが多く見受けられます。ここで強調した『知らない』という部分、はい、そうです、覚えないとか言っておきながら、いきなり覚えましょうというお話です。でも、これはのちにつながる様々な定理や公式を導くために最も重要な約束事であり、とりわけ、三角関数ではこれさえ覚えておけば、以下のような公式を覚える必要は全くありません。

(注)ホンマにこの公式、覚えて完璧に当てはめられますか?私は無理です。。。
生徒にも話していますが、岸谷は本当に覚えていないんですよ、これらの公式は。でも、定義はちゃんと覚えているので、定義に従ってその場で公式を導いて確認して使っています。そもそも、これらの公式が定義から導かれるものなので、間違える道理がありません。一つの重要な事柄=定義を覚えるだけで、無数の公式や定理を覚える必要がなくなります。ほとんどの生徒が1コマの授業でこれらの公式を定義から導けるようになります。定義はそれほどまでに重要な約束事なんです。

割り切って覚えたほうがいい公式もある
先に話題で出した三角関数の加法定理は割り切って覚えましょうと教えることがほとんどです。(難関大学をめざす生徒には証明もできるように指導します。この証明も三角関数の定義と簡単な公式を組み合わせて導出できます。)

(注)2倍角の公式、3倍角の公式、半角の公式、和積の公式、積和の公式、すべて左上の加法定理からすぐに導けます。覚えても良いが、必須ではない。
応用の幅がとても広く、使い勝手が非常に良い定理だからです。20個くらいは別の公式に派生できるでしょうか。こちらも1コマの授業で導けるようになる生徒がほとんどです。

持っている力を最大限使えるような学習をしよう
今回は三角関数を例に挙げましたが、二次関数、数と式・複素数と証明、図形と方程式、数列、ベクトルなどの他の分野も、覚えなくていい公式であふれています。いったいいくつ公式があるか、、、(200個はありますよ汗)覚える数学は効率が悪いんですね。定義は必ず覚えましょう、あとは最小限、応用が利く定理や公式を少しだけ!というのが、いわゆる効率の良い学習ではないかと考えています。せっかく応用できる力を持っているのに、覚える→当てはめることに使っていてはもったいない。定義や重要な定理から導けるようになると、次回お話しする『数読力』の養成にもつながってきます。少しだけ予告をしておくと次回は『数学力=数読力』というテーマでお話できればと準備中です。
ここまでお読みいただき、ありがとうございました。また次回のブログを楽しみにしていてくださいね。





